Consecutive Interior Angles: Definition, Properties, and FAQs

Consecutive interior angles are angles formed by two parallel lines intersected by a transversal. These angles have a unique property that makes them useful in many mathematical contexts. Understanding the definition and properties of consecutive interior angles is essential for solving problems related to geometry, trigonometry, and other fields of mathematics. In this article, we will explore the definition and properties of consecutive interior angles, including their formulas, properties, and FAQs. 

What are Consecutive Interior Angles?

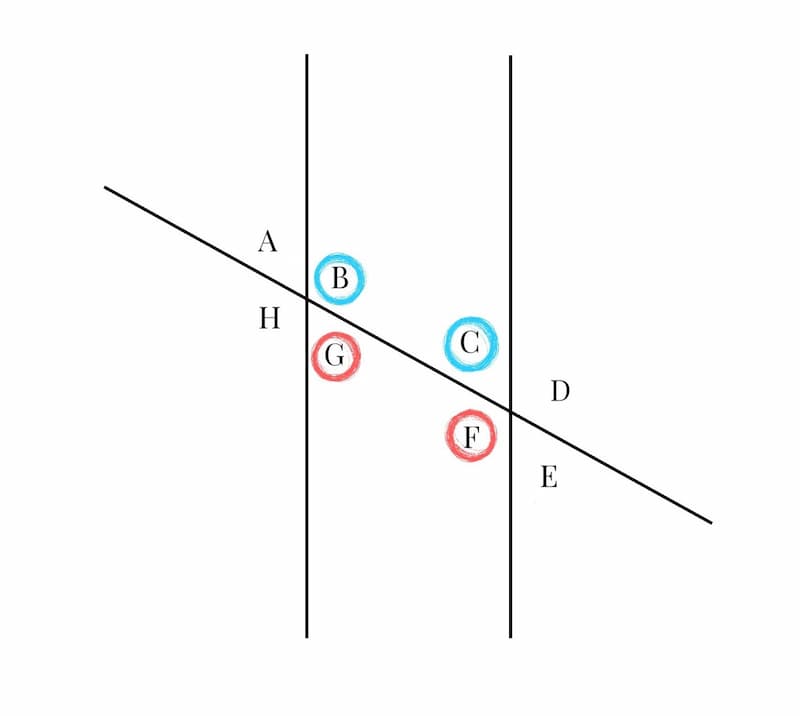
Consecutive Interior Angle Definition

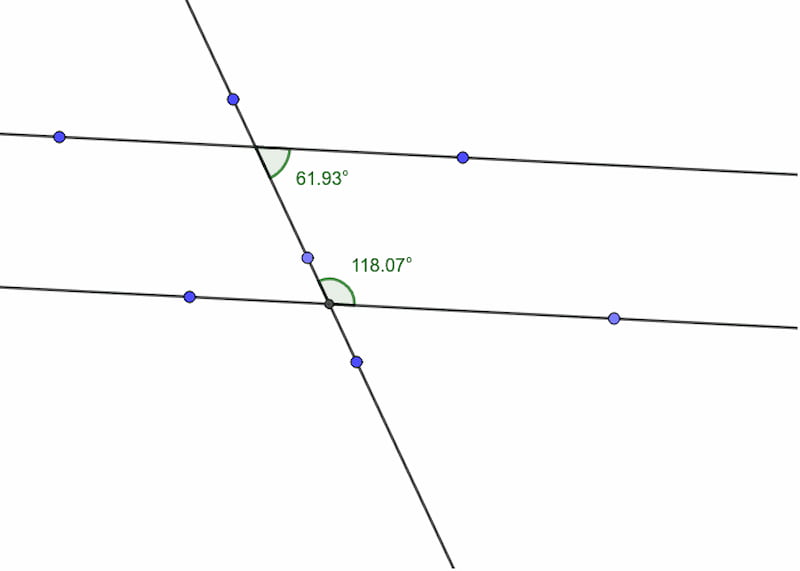
Consecutive interior angles are a pair of angles on the same side of a transversal, and inside (or between) two parallel lines. Specifically, consecutive interior angles are angles that are adjacent (next to each other) and on opposite sides of the transversal.

When two parallel lines are intersected by a transversal, there are eight angles that are formed. The consecutive interior angles are the two angles on the same side of the transversal and are between (or inside) the parallel lines.

Consecutive interior angles are equal in measure when a transversal cuts the two parallel lines. This property can be used to solve problems involving the measurement of angles in parallel lines and transversals diagram.

Consecutive Interior Angle Theorem Proof

The Consecutive Interior Angle Theorem states that when transversal cuts two parallel lines, the consecutive interior angles formed are supplementary (their measures add up to 180 degrees). Here’s proof of this theorem:

Let l and m be two parallel lines cut by a transversal t, and let A and B be two consecutive interior angles formed by t and the parallel lines. We want to show that the sum of the measures of angles A and B is 180 degrees.

First, draw a line perpendicular to both l and t, and label the intersection point C. Then draw a line perpendicular to both m and t and mark the intersection point D. Since l and m are parallel, we know that angles ACD and BDC are also interior angles on the same side of the transversal t, and therefore they are also supplementary (their measures add up to 180 degrees).

Now, we can use the fact that angles ACD and BDC are vertical angles (they share a common vertex and are opposite each other). We know that vertical angles are congruent (have equal measure). Therefore, angle ACD is congruent to angle BDC, and each has measured half the sum of the measures of angles A and B:

ACD = BDC = (A + B) / 2

Since angles ACD and BDC are supplementary, their measures add up to 180 degrees:

ACD + BDC = 180

Substituting the expression for ACD and BDC from above, we get:

(A + B) / 2 + (A + B) / 2 = 180

Simplifying this equation, we get:

A + B = 180

Therefore, the sum of the measures of consecutive interior angles A and B is 180 degrees, which proves the Consecutive Interior Angle Theorem.

Read more >> Volume Of A Triangular Pyramid: Formula & Real-World Applications

Converse of the Consecutive Interior Angle Theorem

The converse of the consecutive interior angle theorem states that if two lines are intersected by a transversal and the consecutive interior angles are supplementary, then the lines are parallel.

To prove the converse of the consecutive interior angle theorem, we assume that the consecutive interior angles are supplementary, and we want to show that the lines are parallel.

Let us consider two lines, line l, and line m, that are intersected by a transversal line t. We are given that ∠1 and ∠2 are consecutive interior angles, and their measures add up to 180 degrees (i.e., they are supplementary). Therefore, we have:

∠1 + ∠2 = 180 degrees

We can rewrite this equation as:

∠1 = 180 degrees – ∠2

Now, let us assume that line l and line m are not parallel. Then, they must intersect at some point P. Let Q be a point on line l and R be a point on line m, such that Q and R are on the same side of line t.

Since line l and line m are not parallel, we know that the angle formed by line l and line t is not equal to the angle formed by line m and line t. Therefore, either ∠1 or ∠2 is not equal to the corresponding consecutive interior angle on the other side.

Without loss of generality, let us assume that ∠1 is not equal to the corresponding consecutive interior angle on the other side. Then, we have:

∠1 ≠ ∠3

Now, let us consider the sum of angles ∠1 and ∠3. Since line l and line m intersect at point P, the sum of the angles ∠1 and ∠3 must be less than 180 degrees (i.e., they form a linear pair):

∠1 + ∠3 < 180 degrees

But we know that ∠1 + ∠2 = 180 degrees, so we can substitute ∠1 with 180 degrees – ∠2:

180 degrees – ∠2 + ∠3 < 180 degrees

Simplifying this inequality, we get:

∠3 < ∠2

But we assumed that ∠1 and ∠2 are consecutive interior angles, which means that ∠3 and ∠2 are corresponding angles. Therefore, if ∠3 is less than ∠2, it implies that line l and line m must be parallel.

Hence, we have shown that if two lines are intersected by a transversal and the consecutive interior angles are supplementary, then the lines are parallel, which is the converse of the consecutive interior angle theorem.

Consecutive Interior Angles Properties

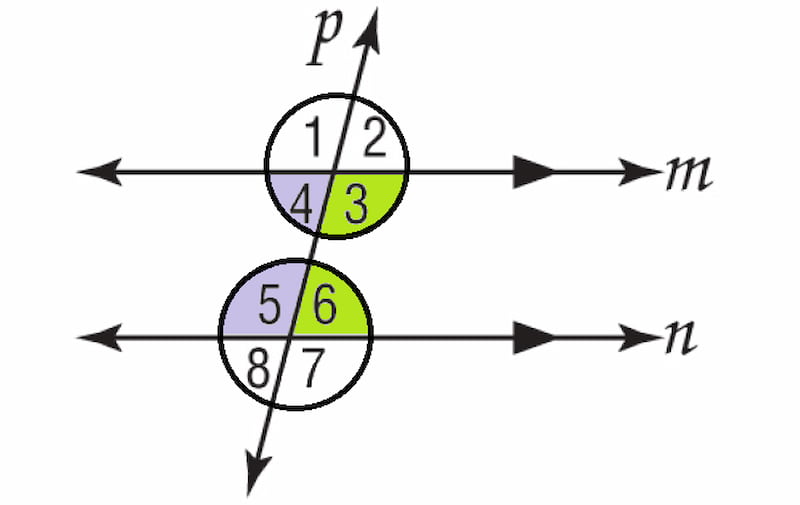
• Consecutive interior angles are a pair of angles on the same side of a transversal and inside two parallel lines. When a transversal cuts two parallel lines, there are eight angles formed. Consecutive interior angles are the two angles that are adjacent (next to each other) and on opposite sides of the transversal.
• Consecutive interior angles are always supplementary. This means that their measures add up to 180 degrees. Mathematically, this can be written as A + B = 180°, where A and B are consecutive interior angles.
• The Consecutive Interior Angle Theorem states that when transversal cuts two parallel lines, the consecutive interior angles formed are supplementary. This theorem is useful in solving problems involving angles formed by parallel lines and a transversal.
• Consecutive interior angles can be used to find missing angle measures in parallel lines and transversal diagrams. For example, if one angle measure is known, the other angle measure can be found by subtracting the known measure from 180 degrees.
• Consecutive interior angles are just one of several types of angles formed by a transversal and two parallel lines. Other types include alternate interior angles, alternate exterior angles, and corresponding angles. These angle pairs have specific relationships to each other, such as being congruent or supplementary, that can be used to solve angle problems in geometry.

Consecutive Interior Angles of a Parallelogram

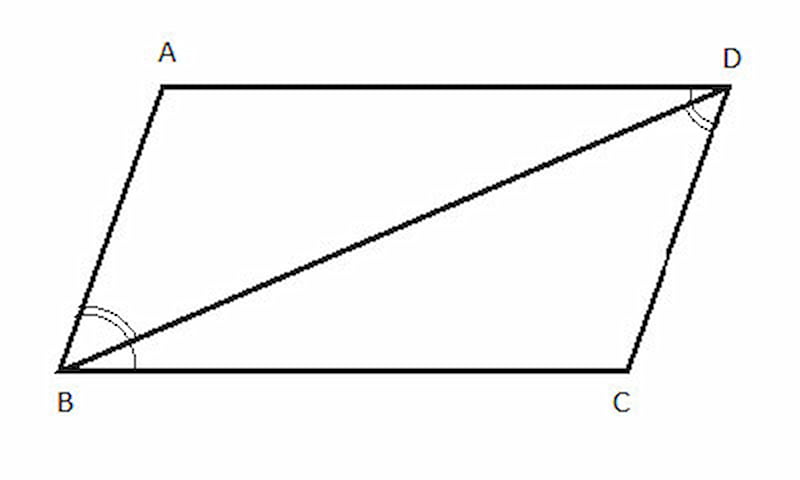
In a parallelogram, the opposite sides are parallel, and the opposite angles are congruent. Therefore, the consecutive interior angles of a parallelogram are also supplementary, meaning that their measures add up to 180 degrees.

To see why this is true, imagine a parallelogram with parallel sides AB and DC and a transversal line that intersects these sides at points E and F, respectively. Then, the consecutive interior angles are ∠AED and ∠DEC, as well as ∠BFE and ∠EFC.

Since AB and DC are parallel, we know that ∠AED and ∠DEC are alternate interior angles and are therefore congruent. Similarly, ∠BFE and ∠EFC are alternate interior angles and are also congruent.

Furthermore, we know that the opposite angles of a parallelogram are congruent, which means that ∠AED is congruent to ∠BFC, and ∠DEC is congruent to ∠EFC.

Since ∠AED is congruent to ∠BFC, and ∠BFE is congruent to ∠EFC, we can conclude that ∠AED and ∠BFE are also alternate interior angles and are therefore congruent. Similarly, ∠DEC and ∠EFC are alternate interior angles and are also congruent.

Therefore, we can see that ∠AED and ∠DEC, as well as ∠BFE and ∠EFC, are pairs of consecutive interior angles that are supplementary, meaning that their measures add up to 180 degrees. This is true for any parallelogram, regardless of its size or shape.

Read more >> Diameter vs Radius: The Relationship Between Them

Are Consecutive Interior Angles Congruent?

One of the common misconceptions about consecutive interior angles is that they are always congruent. However, this is not always the case.

It is important to note that consecutive interior angles are only congruent if the two parallel lines are perpendicular to the transversal. This is due to the fact that perpendicular lines create right angles, which have equal measures of 90 degrees. Therefore, if the two parallel lines are perpendicular to the transversal, the consecutive interior angles are congruent because they are both right angles.

On the other hand, if the two parallel lines are not perpendicular to the transversal, the consecutive interior angles are not congruent. In this case, the consecutive interior angles are supplementary, meaning that their measures add up to 180 degrees. For example, if the two parallel lines are cut by a transversal and the measure of one consecutive interior angle is 100 degrees, then the measure of the other consecutive interior angle will be 80 degrees.

Tips when dealing with Consecutive Interior Angles

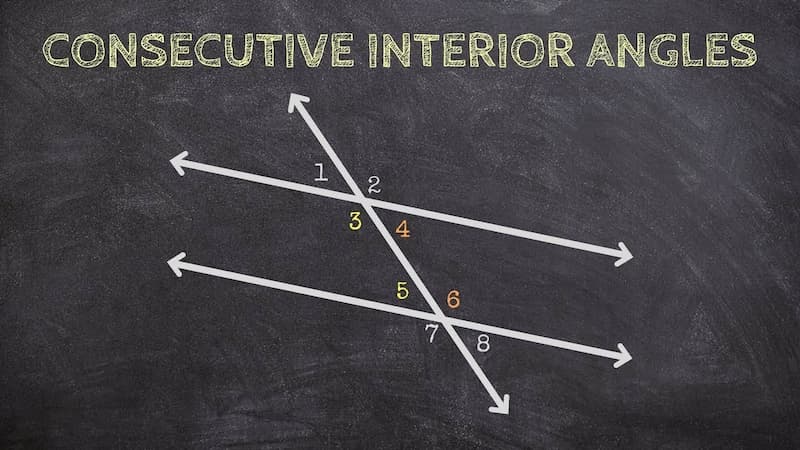
When dealing with math questions about consecutive interior angles, there are a few key things to keep in mind:

• Identify the parallel lines and transversal: Make sure you know which lines are parallel and which line is the transversal. This will help you determine which angles are consecutive interior angles.
• Determine if the parallel lines are perpendicular to the transversal: If the parallel lines are perpendicular to the transversal, then the consecutive interior angles are congruent. If they are not perpendicular, then the consecutive interior angles are supplementary.
• Use algebra to solve for angle measures: If you know the measure of one consecutive interior angle, you can use algebra to solve for the measure of the other consecutive interior angle.
• Use the properties of parallel lines and transversals: Remember the various properties of parallel lines and transversals, such as alternate interior angles, corresponding angles, and vertical angles. These properties can help you determine the measures of various angles in the diagram.
• Draw a clear diagram: It is important to draw a clear and accurate diagram of the given information. This will help you visualize the problem and make it easier to solve.

By keeping these things in mind, you can approach math questions involving consecutive interior angles with greater confidence and accuracy.

FAQs about Consecutive Interior Angles

Here are some frequently asked questions about consecutive interior angles:

What is the Consecutive Interior Angle Theorem?

The Consecutive Interior Angle Theorem states that when transversal cuts two parallel lines, the consecutive interior angles formed are supplementary, meaning that their measures add up to 180 degrees.

Are consecutive interior angles congruent?

Interior angles that are consecutive are not congruent, but they’re supplemental angles. As a transversal line crosses a pair of parallel lines, the total of the consecutive interior angles equals 180 degrees.

How do you find consecutive interior angles?

If a transversal cuts two parallel lines, consecutive interior angles can be found by identifying two angles that are adjacent and on opposite sides of the transversal. The measure of one angle can be subtracted from 180 degrees to find the measure of the other angle, as consecutive interior angles are always supplementary.

What is the relationship between consecutive interior angles and alternate interior angles?

Consecutive interior angles and alternate interior angles are both formed when a transversal cuts two parallel lines. Consecutive interior angles are adjacent and on opposite sides of the transversal, while alternate interior angles are nonadjacent and on opposite sides of the transversal. However, they are congruent with each other.

How can consecutive interior angles be used in problem-solving?

Consecutive interior angles can be used to find missing angle measures in parallel lines and transversal diagrams. The Consecutive Interior Angle Theorem can be used to solve problems involving the measures of consecutive interior angles.

How do consecutive interior angles relate to the interior angles of a polygon?

The sum of the consecutive interior angles of any polygon is (n-2) x 180 degrees, where n is the number of sides of the polygon.

Understanding consecutive interior angles are important for solving problems in geometry, trigonometry, and other areas of mathematics. Overall, by mastering the concepts and properties of consecutive interior angles, we can strengthen our mathematical skills and improve our problem-solving abilities in various fields of mathematics.