Diameter vs Radius: The Relationship Between Them

Diameter and radius are two fundamental terms in mathematics, especially in the study of circles. While both terms are related to the size of a circle, they are not interchangeable, and it’s important to understand the difference between the two. In this blog post, we’ll explore the definitions of diameter and radius, the relationship between the two, and some real-world examples of their applications.

Definition of Diameter vs Radius

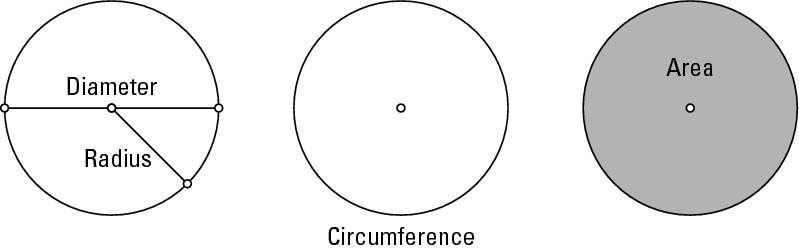
What Is Diameter?

In the realm of geometry, the diameter is a straight line segment that surges through the central core of a circle, connecting two distinct points on the perimeter. This particular segment is regarded as the most prodigious chord of a circle, bifurcating the circle into two mirror-image halves. The length of this aforementioned diametric segment is precise twice the length of the radius, and this numeric value is conventionally represented by the symbol “d.” 

What Is Radius?

Conversely, the radius of a circle refers to a straight line segment that interlinks the nucleus of the circle to any random point on its perimeter. The radius, denoted by the symbol “r,” is one-half of the diameter and is of paramount significance in geometry, as it is instrumental in determining numerous other properties of a circle, such as its area, circumference, and so on.

Comparison Between The Two Terms

Although the diameter and radius are intrinsically related and intertwined, they represent divergent concepts in geometry and are utilized differently. The prime dissimilarity between the diameter and radius is that the former is the most extended chord of a circle that passes through its center, whereas the latter is half the length of the diameter and joins the central point to any point on the perimeter. 

In essence, the radius is the distance from the midpoint to the circumference, while the diameter is the distance across the circle. Another fundamental disparity between the two is that the diameter is perpetual twice the length of the radius. It is vital to grasp this distinction between the two concepts to competently compute the properties of a circle and implement them in practical, real-world scenarios.

Read more >> How to Determine the Measure of a Circle?

Understanding the Relationship between Diameter vs Radius

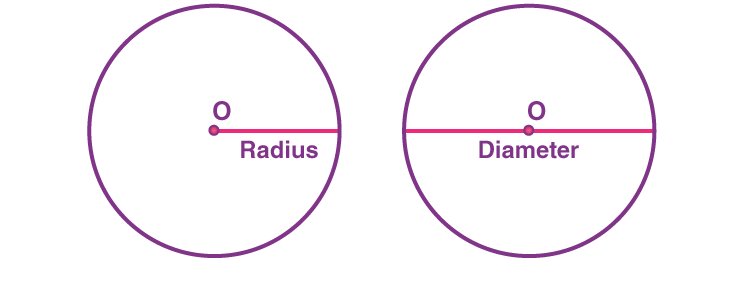
Diameter and radius, two fundamental geometric concepts, are inextricably linked, their intricate relationship forming the foundation of many circular problem-solving applications. Within this section, we will delve into the multifaceted and mathematical formulas for determining the diameter and radius of a circle, as well as explore practical examples of their utilization.

Mathematical Formula For Finding The Diameter Of A Circle Using The Radius

The diameter of a circle, a line segment that traverses the circle’s center and spans its edge, can be calculated based on the circle’s radius. The radius, a line segment extending from the circle’s center to any point on its perimeter, provides a pathway to determine the diameter via the formula:

Diameter = 2 × Radius

In other words, the diameter of a circle can be attained by doubling its radius. For example, if the radius of a circle measures 5 cm, then the diameter is equivalent to 2 times 5, resulting in a diameter of 10 cm.

Mathematical Formula For Finding The Radius Of A Circle Using The Diameter

Conversely, the radius of a circle can be determined with the knowledge of its diameter. The radius of a circle is half of its diameter, which can be mathematically expressed as:

Radius = Diameter ÷ 2

For example, if the diameter of a circle measures 20 m, the corresponding radius is 20 divided by 2, which equals 10 m.

Examples And Applications Of The Formulas

The formulas for determining the diameter and radius of a circle possess a multitude of practical applications. One of which involves calculating the circumference of a circle, which is the distance around its edge. This value can be computed using the formula:

Circumference = π × Diameter

Where π is an unchanging mathematical constant that approximates 3.14. As the diameter is equivalent to twice the radius, another formula for computing the circumference can be derived:

Circumference = 2 × π × Radius

Furthermore, the formulas for diameter and radius can be applied to find the area of a circle, the measure of space encompassed within it. The area can be calculated using the formula:

Area = π × Radius²

or alternatively,

Area = π × (Diameter/2)²

The application of these formulas extends beyond mathematics, finding their usefulness in areas such as engineering, construction, and science. An understanding of these formulas and their practical applications enhances our comprehension of the importance of diameter and radius in various domains.

Read more >> Ray in Math: Definition, Applications, & Examples

Real-World Examples for Diameter vs Radius

Diameter and radius may seem like simple mathematical concepts, but their real-world applications are far-reaching and complex. In this section, we will delve deeper into the ways that diameter and radius are used in construction, transportation, and everyday life, examining the intricate relationships between these measurements and the structures, systems, and objects they inform.

How Diameter And Radius Are Used In Construction

In the high-stakes world of construction, a deep understanding of diameter and radius is critical for success. Builders must not only be able to accurately determine the size of various building materials, such as pipes, beams, and wires, but they must also be able to calculate the curvature of surfaces, the length of arches, and the size of foundations. 

By using intricate mathematical formulas that incorporate diameter and radius, construction professionals can ensure that their structures are not only stable and functional but also aesthetically pleasing and structurally sound.

How Diameter And Radius Are Used In Transportation

In the fast-paced world of transportation, diameter, and radius play a critical role in everything from vehicle design to road construction. For example, the diameter of a wheel has a direct impact on the distance a vehicle will travel with each rotation, which in turn affects speed, distance, and fuel efficiency. 

Meanwhile, the radius of a turn determines the curvature of a road, which is crucial for determining safe driving speeds and avoiding accidents. By taking into account the complex interplay between diameter, radius, and speed, transportation professionals can design transportation systems that are not only efficient but also safe and sustainable.

How Diameter And Radius Are Used In Everyday Life

Even in our daily lives, diameter, and radius have a significant impact. From measuring the distance across a circular object, such as a plate or a pot, to determining the size of a room, the distance from one point to another, or the area of a space that needs to be painted or carpeted, these concepts are crucial for making informed decisions. Moreover, by understanding the intricate relationships between diameter and radius, we can make wise choices when shopping for circular products, such as tires, pots, or furniture, ensuring that we get the right fit for our needs.

Common Misconceptions About Diameter vs Radius

Common Misconceptions about Diameter and Radius

When it comes to mathematical concepts, misunderstandings can arise due to their inherent complexity. Diameter and radius are no exception to this rule, as a number of misconceptions are commonly associated with these terms. One of the most pernicious of these is the idea that the diameter is always twice the length of the radius. While this may be valid in the case of circles, it is not applicable to other shapes.

Another fallacy is the notion that the diameter and radius are essentially the same things. This can be particularly perplexing for newcomers to geometry, as the two terms are often used interchangeably in everyday language. However, mathematically speaking, they denote distinct concepts that cannot be used interchangeably.

A third misunderstanding is that the diameter and radius are exclusive to circles. In reality, these terms are equally relevant to a range of other shapes, including cylinders, spheres, and cones.

Debunking Common Misconceptions

To dispel these misconceptions, it is important to comprehend the mathematical definitions of diameter and radius. As mentioned earlier, the diameter is the length across a circle that passes through its center point, whereas the radius is the length from the center point to any point on the edge of the circle.

Regarding the misconception that the diameter is always twice the length of the radius, it is critical to acknowledge that this only holds true for circles. In other shapes, such as cylinders and cones, the relationship between the diameter and radius will vary.

To combat the misconception that the diameter and radius are identical, one must highlight their differences, even though they are related. This can be accomplished by providing specific instances and using visual aids, such as diagrams and illustrations, to illustrate the distinction between the two.

Lastly, to challenge the notion that the diameter and radius only apply to circles, it is imperative to extend the discussion to other shapes that can be described using these terms. For example, the radius of a sphere is the distance from its center to any point on its surface, whereas the diameter is the length across the sphere, passing through the center point.

By addressing these common misconceptions and providing detailed explanations and examples, students can develop a thorough understanding of the difference between diameter and radius. This will prevent confusion and mistakes when working with these concepts in mathematics.

Exercises and Problems with Diameter and Radius

A remarkable way to help students truly apprehend the difference between diameter and radius is to engage them in praxis-oriented exercises and sample problems. Such exercises are a proven method to reinforce students’ knowledge of the concepts they have learned and to prepare them for more complex mathematical concepts.

Below are some practice exercises, specifically designed to aid students in understanding the difference between diameter and radius:

1. Compute the diameter of a circle with a radius of 7cm.
2. Determine the radius of a circle with a diameter of 14m.
3. If a circle has a diameter of 12cm, what is its radius?
4. If a circle has a radius of 10ft, what is its diameter?

These exercises offer students an opportunity to strengthen their grasp of the mathematical formulas used to determine the diameter and radius of a circle. By working through these problems, students can practice the application of the formulas and enhance their confidence in their ability to utilize them.

Apart from practice exercises, students can be provided with sample problems to solve on their own. These problems entail the application of the concepts they have learned and the development of problem-solving skills. Here are some sample problems that students can tackle:

1. A circular swimming pool has a diameter of 10 meters. What is its radius?
2. A pizza has a diameter of 20 inches. What is its radius?
3. A bicycle wheel has a radius of 35 cm. What is its diameter?
4. A circular garden has a diameter of 15 ft. What is its radius?

These problems can be used to challenge students and urge them to think critically about the relationship between diameter and radius. Through these problems, students can hone their problem-solving skills and learn how to apply mathematical concepts in real-life scenarios.

Conclusion

In conclusion, understanding the difference between diameter and radius is crucial for anyone studying mathematics. While they are related, diameter and radius represent different concepts in geometry and have different applications in the real world. By exploring the definitions, formulas, examples, and common misconceptions, we hope that this blog post has helped to clarify the difference between the two terms and provided a solid foundation for further study.