Scan QR code or get instant email to install app

Question:
1212Which of the following answer choices accurately matches each function with its corresponding solution or factored form?
1) 
2) 
3) 
A
12121)  and
and 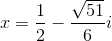
2) x = 5 and and
and 
3)
 and
and 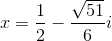
2) x = 5 and
 and
and 
3)

explanation
1212Use any appropriate factoring method to factor and solve the equations given.
Rewrite the first equation into the general quadratic form:
 . Use the quadratic formula to solve for x:
. Use the quadratic formula to solve for x:
 , with a = 3, b = -3, c = 5.
, with a = 3, b = -3, c = 5.
 , and
, and
 , so
, so
 and
and  .
.
Rewrite the second equation as a difference of cubes:
 and apply the general factor form of difference of cubes
and apply the general factor form of difference of cubes  to find:
to find:
 , set both expressions equal to 0:
, set both expressions equal to 0:
x - 5 = 0 so x = 5 and  , which requires the quadratic formula:
, which requires the quadratic formula:
 which becomes
which becomes
 , which becomes
, which becomes
 and
and  .
.
Begin the third function by factoring the GCF,  :
:
 . The expression in parentheses should be recognized as a difference of squares, which can be factored using the general form of
. The expression in parentheses should be recognized as a difference of squares, which can be factored using the general form of  . So:
. So:

Take more free practice tests for other PASSEMALL topics with our accuplacer practice now!
Related Information

Comments