1212Which answer provides the solution to this system of equations and describes the relationship between the lines? 0 = -6y - 10 + 2x

1212The solution to the system of equations is the point, or collection of points, that exists on both lines. If the lines do not intersect there is no solution, they share the same slope, and they are parallel. If the lines intersect once, there is one solution, and the lines can be perpendicular if their slopes are negative reciprocals of each other. If the lines intersect at every point, there is an infinite number of solutions, and they are the same line; this happens when the lines are multiples of each other. Solve the system using any method, here we will use substitution after solving each equation for y. Solving the first equation: , multiply both sides by 20 to eliminate the denominator: 5y + 10 = -12x + 8, combine like terms and isolate y: 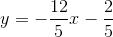Solve the second equation for y: 0 = -6y - 10 + 2x, add 6y to both sides and divide both sides by 6 and reduce: The relationship between the lines can be determined by comparing the slopes: Slope 1 = Slope 2 = , the slopes are neither the same nor negative reciprocals, so there is one solution to the system and the lines are neither parallel nor perpendicular. To solve the system, substitute the expression for y of one equation into the y variable of the other equation: , multiply the equation by LCM 15 to eliminate the denominators: -36x - 6 = 5x - 25, combine like terms and isolate x: . Substitute this value for x into either equation to solve for y: , which becomes . The solution is .