How to Determine the Measure of a Circle?

The measure of a circle is an important concept in mathematics, and it is used in a variety of fields, from engineering to architecture. The measure of a circle refers to its circumference, which is the distance around the circle. Determining the measure of a circle is essential in calculating the size of circular objects and understanding their properties. In this article, we will discuss the different methods for determining the measure of a circle.

What is a Circle?

A circle is a two-dimensional shape that is defined as a set of points that are equidistant from a fixed point, called the center. The distance between the center and any point on the circle is called the radius. Alternatively, a circle can be defined as the locus of all points that are at a fixed distance (the radius) from a given point (the center) in a two-dimensional plane. Circles are often depicted using the Greek letter “π” (pi) to represent the ratio of the circle’s circumference (the distance around the circle) to its diameter (the distance across the circle, passing through the center). 

The Measure of a Circle

Radius and Diameter of a Circle

The radius and diameter of a circle are fundamental measurements used to describe the size and shape of a circle. The radius is the distance from the center of the circle to any point on its circumference, while the diameter is the distance across the circle, passing through its center. The radius is typically denoted by the letter “r”, while the diameter is denoted by the letter “d”. The relationship between the radius and diameter is simple: the diameter is always twice the length of the radius or d = 2r.

To calculate the circumference of a circle, you can use the formula C = 2πr, where C represents the circumference and π (pi) is a mathematical constant approximately equal to 3.14. This formula can be rearranged to solve for the radius or diameter of a circle, depending on which measurement is known.

For example, if the circumference of a circle is known to be 20 units, the radius can be calculated as follows:

C = 2πr

20 = 2πr

r = 20/(2π)

r ≈ 3.18 units

Alternatively, if the diameter of a circle is known to be 10 units, the radius can be found using the relationship between radius and diameter:

d = 2r

10 = 2r

r = 10/2

r = 5 units

The radius and diameter of a circle are essential measurements used to calculate its circumference, area, and other properties. The formula for the circumference of a circle involves the radius, while the relationship between the radius and diameter is straightforward.

Read more >> Ray in Math: Definition, Applications, & Examples

Circumference of a Circle

The circumference of a circle is the distance around its outer edge or boundary. It is a fundamental concept in geometry and is used in many mathematical and real-world applications. The circumference of a circle can be calculated using the formula:

Circumference = 2πr = πd

where “r” is the radius of the circle and “π” (pi) is a mathematical constant approximately equal to 3.14.

For example, suppose we have a circle with a radius of 5 cm. We can find the circumference by using the formula:

Circumference = 2πr = 2π(5) = 10π ≈ 31.4 cm

Therefore, the circumference of the circle is approximately 31.4 cm. It is important to note that the units of the radius and circumference must be the same for the calculation to be valid.

The circumference of a circle is also related to the diameter of the circle. The diameter is the distance across the circle passing through the center. It is twice the length of the radius. Therefore, the formula for the circumference of a circle can also be written as C = πd, where d is the diameter of the circle.

For example, if a circle has a diameter of 10 cm, the circumference can be found by using the formula C = πd, where d = 10 cm. Plugging in the values, we get C = π(10) = 10π ≈ 31.4 cm. Therefore, the circumference of the circle is approximately 31.4 cm.

Are of a Circle

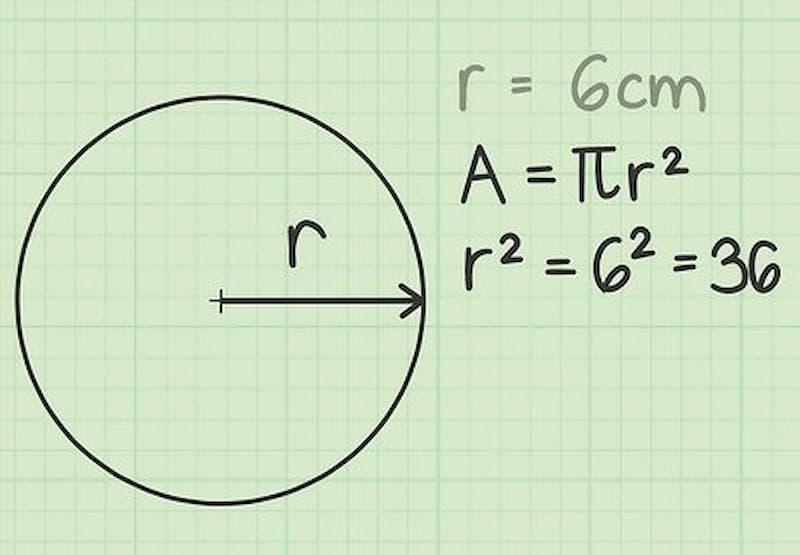
The area of a circle is the measure of the region enclosed by a circle in a two-dimensional plane. It is denoted by the letter “A” and is measured in square units. 

The formula to find the area of a circle is A = πr^2, where “r” is the radius of the circle and π (pi) is a mathematical constant with a value of approximately 3.14. The radius is the distance from the center of the circle to any point on the circumference. Therefore, the area of a circle depends only on its radius, and not on its circumference or diameter.

To calculate the area of a circle, we can follow these steps:

• Identify the radius of the circle.
• Square the radius by multiplying it by itself (r x r).
• Multiply the result obtained in step 2 by π (pi).

For example, let’s find the area of a circle with a radius of 4 units. Using the formula, we have:

A = πr^2

A = π(4)^2

A = 16π

Therefore, the area of a circle with a radius of 4 units is 16π square units.

It is important to note that the formula for the area of a circle can also be expressed in terms of the diameter of the circle. Since the diameter is twice the radius, we can substitute 2r for d in the formula. Thus, the formula for the area of a circle can also be written as A = π(d/2)^2. However, it is more common to use the formula A = πr^2 when dealing with circles.

Read more >> Consecutive Interior Angles: Definition, Properties, and FAQs

Arc Length of a Circle

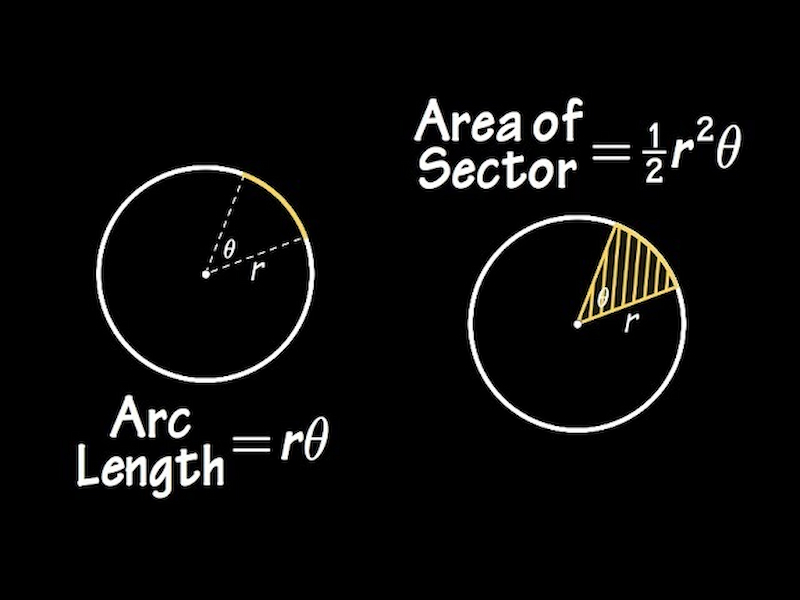
The arc length of a circle is defined as the length of the portion of the circle’s circumference that is intercepted by a central angle. In other words, it is the length of the arc that makes up a given portion of the circle. The arc length is usually measured in linear units such as centimeters, inches, or feet.

The formula for the arc length of a circle is given:

Arc length = (central angle/360) x 2πr

where r is the radius of the circle, and the central angle is measured in degrees.

For example, if we want to find the arc length of a circle with a radius of 5 cm and a central angle of 60 degrees, we can use the formula as follows:

Arc length = (60/360) x 2π(5)

Arc length = (1/6) x 10π

Arc length = 5/3π cm (approximately 5.24 cm)

Another example would be finding the arc length of a circle with a radius of 8 inches and a central angle of 135 degrees:

Arc length = (135/360) x 2π(8)

Arc length = (3/8) x 16π

Arc length = 6π inches (approximately 18.85 inches)

The arc length of a circle is an important concept in geometry and is used in various real-world applications such as in construction, engineering, and design. For example, architects and engineers use arc length to determine the length of curved surfaces, such as the length of an arch or the curvature of a bridge.

Sector Angle of a Circle

A sector of a circle is a region bounded by two radii and an arc of the circle. The angle formed by the two radii is called the sector angle, and it is measured in degrees or radians. The sector angle determines the size of the sector and the length of the arc it encompasses.

The formula for the area of a sector is given by:

Area of sector = (sector angle / 360) x πr²

where r is the radius of the circle.

Similarly, the formula for the arc length of a sector is given by:

Arc length = (sector angle / 360) x 2πr

where r is the radius of the circle.

For example, suppose we have a sector of a circle with a radius of 6 cm and a sector angle of 45°. To find the area of the sector, we use the formula:

Area of sector = (45° / 360) x π(6 cm)²

= 0.125 x 36π

= 4.5π cm²

To find the arc length of the sector, we use the formula:

Arc length = (45° / 360) x 2π(6 cm)

= 0.125 x 12π

= 1.5π cm

Therefore, the area of the sector is 4.5π cm² and the arc length of the sector is 1.5π cm.

Inscribed Angles of a Circle

The inscribed angle of a circle is an angle formed by two chords of a circle that have a common endpoint on the circle. The vertex of the angle is located on the circle, while the sides of the angle are the chords of the circle.

The formula to find the measure of an inscribed angle is:

Angle measure = ½ (central angle measure)

where the central angle is the angle subtended by the same arc as the inscribed angle.

For example, if a central angle measures 120 degrees, the inscribed angle it subtends will measure 60 degrees (½ of 120 degrees).

Inscribed angles have several properties that are useful in solving geometry problems. Some of these properties include:

• Inscribed angles that subtend the same arc are congruent.
• An inscribed angle is half the measure of its corresponding central angle.
• The measure of an inscribed angle is equal to half the difference between the measures of the intercepted arcs.

How to Use the Measure of a Circle in Daily Life?

The measure of a circle can be used in many practical applications in daily life. Here are a few examples:

• Construction: The measure of a circle is essential for construction workers, architects, and engineers when designing and building structures that require circular shapes such as bridges, water tanks, and silos.
• Art and Design: Artists and designers often use circular shapes in their work, and the measure of a circle can help them calculate the size and proportions of these shapes.
• Navigation: Maps and compasses use the measure of a circle to help people navigate and find their way. The degree measurements on a compass are based on the circle’s 360-degree measurement.

These are just a few examples of how the measure of a circle can be used in daily life. In general, understanding the properties of circles and their measurements can be useful in many practical and theoretical applications.

How to Remember the Measure of a Circle?

Here are some tips that might help you remember this formula:

• Memorize the formula: One of the simplest ways to remember the formula for the circumference of a circle is to simply memorize it. Write it down on a piece of paper and repeat it several times until it becomes familiar to you. Over time, you will be able to recall the formula without having to think too hard about it.
• Use a mnemonic device: Another way to remember the formula is to use a mnemonic device. This is a technique that helps you remember something by associating it with something else that is easier to remember. For example, you could use the phrase “Circumference equals two pi r” to help you remember the formula. You might also come up with your own mnemonic device that is more personalized to your learning style.
• Visualize a circle: Another way to remember the formula is to visualize a circle with a radius and imagine measuring its circumference using a tape measure that wraps around it twice. You can also draw a picture of a circle with the radius and circumference labeled to help you visualize the relationship between them.

Final Words

In conclusion, determining the measure of a circle is an important skill that has many practical applications. By understanding the different methods for determining the measure of a circle, including the use of formulas and tools, you can gain a deeper appreciation for the properties of circular objects and the important role they play in our daily lives.