A right circular cylinder is a three-dimensional object with a circular base and straight, parallel sides that culminate in another circular base. It is a common shape in many everyday objects, from soda cans to water tanks. Finding the volume of a right circular cylinder is an important skill in geometry and engineering, as it can help in determining the amount of space or capacity an object can hold. Calculating the volume of a right circular cylinder is a straightforward process that involves the use of a simple formula, and this topic is explored in detail in this article.
What is a Right Circular Cylinder?
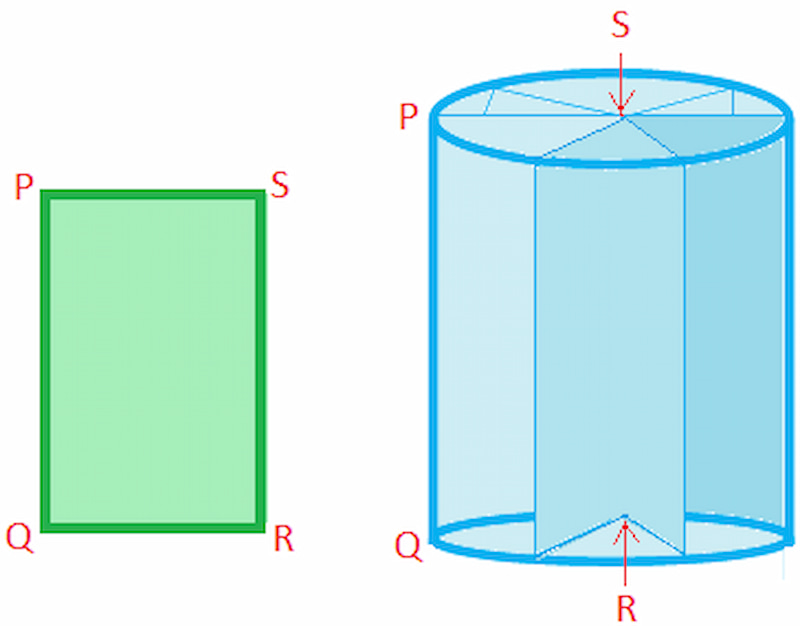
A right circular cylinder is a three-dimensional geometric shape that consists of two congruent circular bases and a curved lateral surface that connects the bases. The axis connecting the centers of the circular bases is perpendicular to the bases, and the lateral surface is formed by straight lines connecting the points on the bases to form a curved surface. If the axis connecting the centers of the bases is perpendicular to the plane of the bases, the cylinder is called a right circular cylinder. Right circular cylinders are commonly used in engineering and architecture, such as in the design of pipes, tubes, and storage tanks.
The Volume of a Right Circular Cylinder
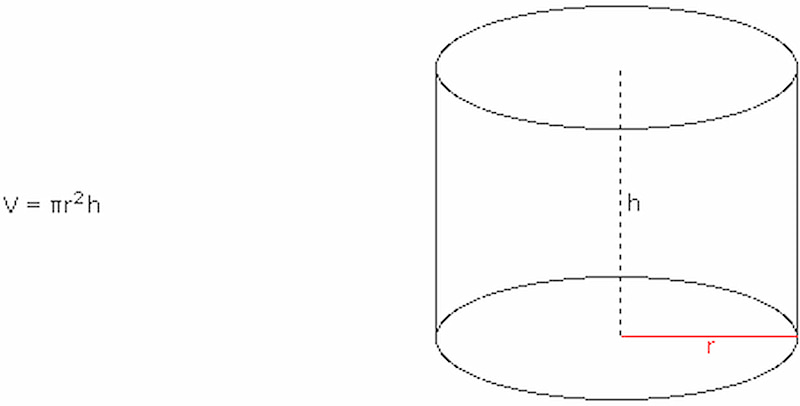
Formula
The volume (V) of a right circular cylinder can be calculated using the formula:
V = πr^2h
where r is the radius of the circular base of the cylinder, h is the height of the cylinder, and π (pi) is a mathematical constant approximately equal to 3.14159.
To calculate the volume of a right circular cylinder, you need to know the values of r and h. First, square the radius (r) of the circular base, then multiply the squared radius by the height (h) of the cylinder and finally multiply the result by π. The unit of measurement for the volume will be the cube of the unit of measurement for the radius and height.
For example, if a cylinder has a radius of 3 cm and a height of 6 cm, its volume can be calculated as follows:
V = πr^2h
V = π(3 cm)^2(6 cm)
V = π(9 cm^2)(6 cm)
V = 54π cm^3
Therefore, the volume of the cylinder is 54π cubic centimeters.
Read more >> Volume Of A Triangular Pyramid: Formula & Real-World Applications
Principle of the Volume of the Right Circular Cylinder
The principle for calculating the volume of a right circular cylinder is based on the fact that the volume of any three-dimensional shape is the product of the area of the base and the height of the shape. For a right circular cylinder, the base is a circle, and the height is the distance between the two circular bases.
To calculate the volume of a right circular cylinder, we first need to find the area of the base, which is a circle. The area of a circle is given by the formula A = πr^2, where r is the radius of the circle. Once we have found the area of the circular base, we multiply it by the height of the cylinder to get the volume.
So, the formula for the volume of a right circular cylinder is V = πr^2h, where V is the volume, r is the radius of the circular base, and h is the height of the cylinder. We can use this formula to find the volume of any right circular cylinder, as long as we know the values of the radius and height.
It is important to note that the units of measurement for the radius and height should be consistent when calculating the volume. For example, if the radius is measured in centimeters, and the height is measured in meters, then the volume should be expressed in cubic meters. Additionally, when rounding the answer, we should make sure to keep an appropriate number of significant figures, depending on the precision of the measurements.
How To Find the Volume of the Right Circular Cylinder by Steps?
To find the volume of a right circular cylinder, follow these steps:
Step 1: Identify the radius (r) and height (h) of the cylinder.
The radius (r) is the distance from the center of the circular base to any point on the edge of the base, and the height (h) is the distance between the circular bases along the axis of the cylinder.
Step 2: Square the radius (r) of the circular base. This gives you r^2.
To square a number, you multiply it by itself. So, r^2 = r × r. For example, if the radius is 4 cm, then r^2 = 4 × 4 = 16 cm^2.
Step 3: Multiply the squared radius (r^2) by the height (h) of the cylinder. This gives you the product r^2h.
To find the product of two numbers, you multiply them together. So, r^2h = r^2 × h. For example, if the height is 10 cm, then r^2h = 16 cm^2 × 10 cm = 160 cm^3.
Step 4: Multiply the product r^2h by π (pi). This gives you the volume (V) of the cylinder.
π (pi) is a mathematical constant that is approximately equal to 3.14159. To multiply a number by π, you can use a calculator or estimate π to a reasonable number of decimal places. So, V = πr^2h. For example, if π is approximated to 3.14, then the volume of the cylinder with a radius of 4 cm and a height of 10 cm is V = 3.14 × 16 cm^2 × 10 cm = 502.4 cm^3.
Step 5: Include the correct unit of measurement for the volume.
The unit of measurement for the volume is the cube of the unit of measurement for the radius and height. For example, if the radius is measured in centimeters and the height is measured in meters, then the volume will be measured in cubic centimeters. Make sure to include the correct unit in your final answer.
Solved Examples of the Volume of the Right Circular Cylinder

Here are some solved examples of the volume of a right circular cylinder:
Example 1: Find the volume of a cylinder with a radius of 5 cm and a height of 10 cm.
Solution:
- Step 1: Identify the values of r and h. Here, r = 5 cm and h = 10 cm.
- Step 2: Calculate the area of the base. A = πr^2 = π(5 cm)^2 = 25π cm^2.
- Step 3: Multiply the area of the base by the height. V = Ah = 25π cm^2 x 10 cm = 250π cm^3.
Therefore, the volume of the cylinder is 250π cubic centimeters.
Example 2: A cylindrical water tank has a radius of 2 m and a height of 8 m. What is the volume of water that can be stored in the tank if it is filled to capacity?
Solution:
- Step 1: Identify the values of r and h. Here, r = 2 m and h = 8 m.
- Step 2: Calculate the area of the base. A = πr^2 = π(2 m)^2 = 4π m^2.
- Step 3: Multiply the area of the base by the height. V = Ah = 4π m^2 x 8 m = 32π m^3.
Therefore, the total volume of the cylindrical tank is 32π m^3.
Example 3: A metal pipe has an outer diameter of 10 cm and a length of 30 cm. What is the volume of the metal used in the pipe, assuming the thickness of the pipe is 2 mm?
Solution:
- Convert the thickness of the pipe to centimeters: 2 mm = 0.2 cm.
- Calculate the inner diameter of the pipe: 10 cm – 0.2 cm – 0.2 cm = 9.6 cm.
- Calculate the radius of the pipe: 4.8 cm.
- Calculate the volume of the outer cylinder: π(5 cm)^2(30 cm) = 750π cm^3.
- Calculate the volume of the inner cylinder: π(4.8 cm)^2(30 cm) = 691.2π cm^3.
- Calculate the volume of the metal used in the pipe: 750π cm^3 – 691.2π cm^3 = 58.8π cm^3.
Therefore, the volume of the metal used in the pipe is 58.8π cubic centimeters.
Read more >> Diameter vs Radius: The Relationship Between Them
How Can the Volume of the Right Circular Cylinder be Used in real-life applications?

The volume of a right circular cylinder has many real-life applications, some of which are:
- Water tanks: The volume of a right circular cylinder is used to calculate the amount of water that can be stored in a cylindrical water tank. This helps in designing and constructing water tanks of various sizes to meet different water storage needs.
- Hydraulic systems: The volume of a right circular cylinder is used in hydraulic systems, where the cylinder is filled with a fluid such as oil or water, and pressure is applied to move a piston or other mechanical components. The volume of the cylinder helps in determining the amount of fluid needed to achieve a specific amount of pressure or force.
- Manufacturing: The volume of a right circular cylinder is used in manufacturing to calculate the amount of material needed to create cylindrical objects. This helps in designing and producing objects such as pipes, rollers, and cylinders of different sizes and dimensions.
- Packaging: The volume of a right circular cylinder is used in designing and manufacturing packaging materials such as cans, bottles, and tubes. The volume helps in determining the amount of product that can be contained in the packaging and ensures that the packaging is designed to fit the product correctly.
- Construction: The volume of a right circular cylinder is used in construction to calculate the amount of concrete or other materials needed to construct cylindrical structures such as columns and pillars. This helps in ensuring that the structure is sturdy and meets the required specifications.
FAQs about the Volume of the Right Circular Cylinder
Here are some frequently asked questions about the volume of the right circular cylinder:
How do you find the radius of a cylinder if you know the volume and height?
To find the radius of a cylinder if you know the volume and height, you can rearrange the formula for the volume of a cylinder to get r = √(V/πh). This formula can be used to calculate the radius of the circular base if you know the volume and the height of the cylinder.
What Is the difference between the formula of the cylinder and the right circular cylinder?
The formula for a cylinder is V = Bh, where B is the area of the base and h is the height of the cylinder. This formula can be used to find the volume of any cylinder, regardless of whether it is a circular cylinder or not. However, the formula for a right circular cylinder is V = πr^2h, where r is the radius of the circular base. This formula is specific to right circular cylinders, which have circular bases and straight sides that are perpendicular to the base.
How do you find the volume of a cylinder if only base area and height are given?
If the base area and height of a cylinder are given, you can use the formula V = Bh to find the volume. Simply multiply the base area by the height to get the volume. For example, if the base area is 25 square units and the height is 10 units, the volume would be V = 25 x 10 = 250 cubic units.
In conclusion, calculating the volume of a right circular cylinder is a simple and essential skill in geometry and engineering. With the formula V = πr²h, finding the volume of a cylinder requires only two measurements, the radius of the base and the height. This formula can be applied in various real-life situations, from measuring the volume of liquid in a cylindrical container to determining the capacity of a cylindrical storage tank.

PCCN vs CCRN: Which Certification Should I Take?
In this discussion, we will examine the fundamental distinctions between PCCN vs CCRN certifications, allowing you to make an informed and right decision about which certification is best for your nursing career progression.
June 20, 2023

Is PCCN Worth It? A Comprehensive 2024 Study Guide
In this article, we will provide all the enrollment criteria, how to apply, whether is PCCN worth it for you to obtain, and how to get a high mark.
June 20, 2023

PCCN Requirements - How to Become a Progressive Care Certified Nurse?
To become a progressive care nurse, you must first obtain the PCCN certification. This post will help you understand PCCN certification, PCCN requirements, and efficient approaches to obtaining this certification.
June 20, 2023
