Scan QR code or get instant email to install app
Question:
1212Spherical capacitance, C, is defined as the ratio of the product of 4, π, vacuum permittivity,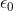 
, and Coulomb's constant, k to the difference between the ratio of 1 to the radial length a, and the ratio of 1 to the radial length b. Which of the following correctly solves spherical capacitance for radial length b?
A
1212
explanation
1212Begin by translating the given definition into an algebraic expression.
Manipulate the equation to solve for b:
Multiply both sides by the denominator:
, divide both sides by C:
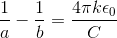, solve for 
, combine the right hand side using the common denominator:
, and evaluate the reciprocal of each side to find b:
Take more free practice tests for other PASSEMALL topics with our accuplacer practice test now!
Related Information
Comments