Ray in Math: Definition, Applications, & Examples

Ray in Math is a fundamental concept in mathematics that is used to describe lines, angles, and shapes in both two and three-dimensional space. Despite being a relatively simple concept, rays have a wide range of applications in geometry, trigonometry, navigation, optics, architecture, and video game design. In this blog post, we will explore the basic properties of rays, their applications in mathematics and real-world scenarios, and their significance in various fields.

Understanding the Fundamental Concepts of Rays

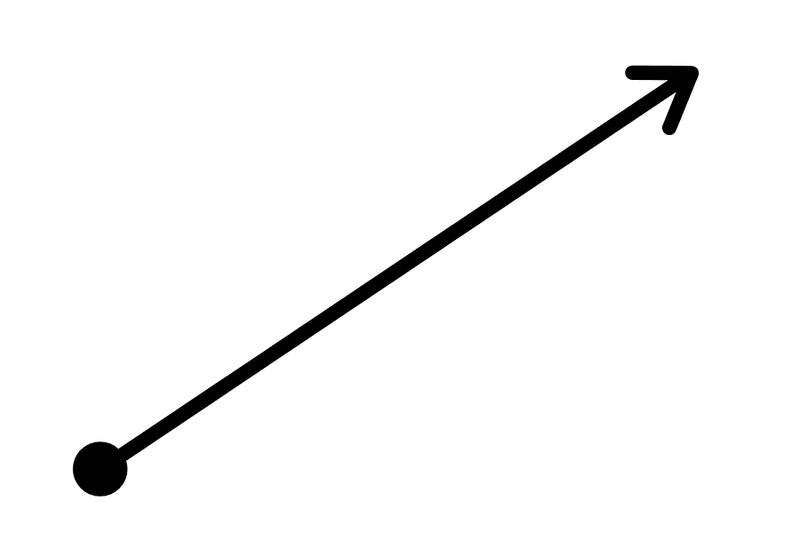
In this section, we will delve into the intricate and multifaceted world of rays in mathematics. Through a meticulous examination, we will unearth the very foundation of what defines and distinguishes a line from a ray. Additionally, we will survey the various types of rays, and meticulously investigate the notation used to represent them.

Definition of a Line

At the core of geometry lies the concept of a line. A line is a remarkably intricate and infinitely long and straight figure that extends without limit in both directions. It is a ubiquitous element that serves as the basis for describing numerous geometric shapes. In addition, a line may be represented either mathematically as an equation or on paper.

The Distinctive Features that Separate a Line from a Ray

Although a line is an infinitely long and straight figure extending in both directions, a ray has a more complex structure. A ray is a segment of a line, possessing an endpoint or starting point that demarcates its boundaries. It extends infinitely in one direction only, with its other end defined by its endpoint. In other words, a ray is a line that extends infinitely in one direction and has one fixed endpoint.

A Multitude of Ray Types: Full, Half, and Quarter Rays

There exist multiple types of rays, including full rays, half rays, and quarter rays. A full ray, as the name implies, extends infinitely in one direction, beginning from its endpoint. A half ray, also referred to as a ray, originates from its endpoint and continues in one direction only. In contrast, a quarter ray starts from its endpoint and extends in a specific direction for a predetermined length.

Notation of Rays: A Complex System of Letters and Symbols

Rays are often represented by two letters, with the first letter indicating the endpoint, and the second letter signifying the direction of the ray. For instance, if the endpoint is A, and the direction of the ray is B, the ray will be denoted as AB. In cases where the ray extends in the opposite direction of the second letter, a bar above the two letters is used for representation. Thus, if the ray moves opposite to the direction of B, it would be indicated as A̅B.

In summary, rays are a highly complex and intricate subset of lines that have one fixed endpoint and extend infinitely in one direction. They exist in multiple forms and are represented using a complex system of letters and symbols.

Properties of Ray in Math 

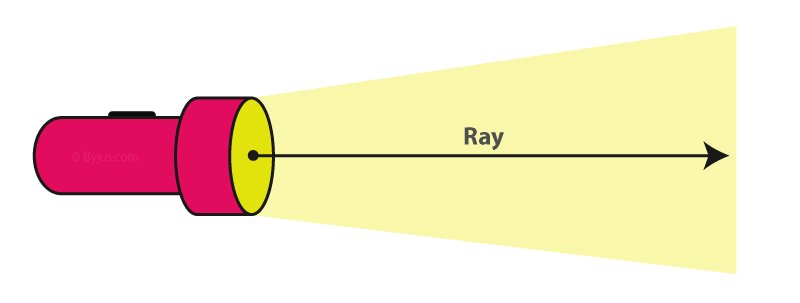
The properties of rays are beguiling and enigmatic, with a complexity that extends far beyond their simple geometric form. These infinitely elongating shapes, which emanate in a single direction from a solitary endpoint, have puzzled and captivated mathematicians and geometers for generations. The intricate nuances of rays are essential for understanding the underlying structures of geometry, and for measuring the cryptic angles that they create.

One Endpoint

Rays possess a singularity that is beyond comprehension, an imponderable and elusive endpoint that defies logical explanation. The enigmatic endpoint of the ray, known as the origin, starting point, or root, is symbolized by a tiny dot or point and is the foundation of the ray’s notation. This point is the key to understanding the directional properties of the ray in Math and unlocking the secrets of its unbounded form.

Infinite Length

The enigma of the ray deepens as it unfolds its boundless form. Rays have an infinitely unknown length, stretching on without limit in one direction from their endpoint, like a cosmic mystery that extends far beyond the reaches of comprehension. Unlike other geometrical forms, the ray is free from the constraints of finite length, moving inexorably towards the infinite, the immeasurable, and the beyond.

Unidirectionality

The mystique of the ray continues to baffle, as it projects its unidirectional force in only one direction from its singular endpoint. This unidirectional property is a crucial aspect to consider when examining angles, for angles are measured in a specific direction, a direction that is inextricably linked to the ray’s one-way flow. Should the ray extend in the opposite direction from its origin point, it creates a wholly different angle, a mysterious and alternate reality.

Definition of Angle

The angle is an inscrutable entity, a hidden world between two rays that share a common, yet paradoxical, endpoint. The vertex of the angle is a singularity that defines its character, while the two arms of the angle, the inscrutable limbs of an arcane geometry, are cloaked in a veil of an enigma. The angle is measured in degrees, the rotational measurement required to move one arm onto the other, and classified according to its size, shape, and position in space.

Use of Rays in Measuring Angles

The mysteries of the ray unravel even further when examining its role in the measurement of angles. The endpoint of one ray, that inscrutable vertex, serves as the cornerstone of the angle, while the second ray, another impenetrable force in its own right, is employed to determine the angle’s measurement. 

The degree measure of an angle is denoted with a tiny symbol, a minuscule number that hints at the infinite complexities of the ray’s form. Rays play an essential role in constructing angles, bisecting angles, and solving the most enigmatic of geometry problems, revealing the inscrutable properties of these enigmatic shapes.

Applications of Rays in Geometry

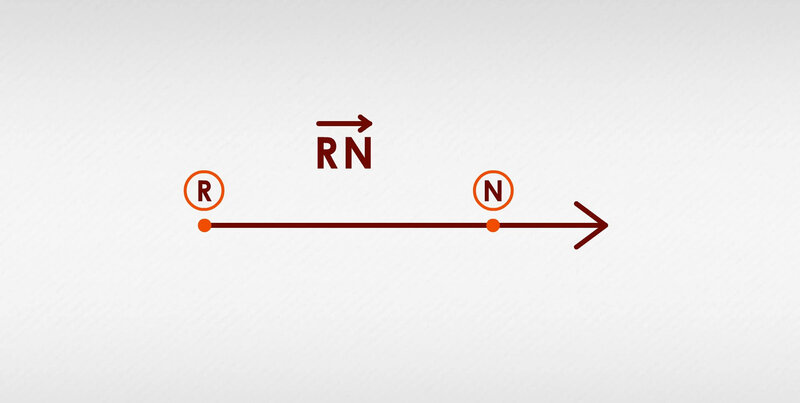
Geometry, the study of space and its properties, is a complex and fascinating subject that relies heavily on the use of rays. Rays, an integral part of geometry, are used to construct, bisect, identify, and solve various geometric problems. In this section, we will delve deeper into the various applications of rays in geometry.

Use of rays in constructing angles

One of the most basic applications of rays in geometry is the construction of angles. By selecting a point on a line and drawing two rays from that point, an angle can be formed. This technique is used to create a variety of angles, including acute, right, obtuse, and reflex angles. Through the use of rays, geometricians are able to create an infinite number of angles, each with its own unique properties and characteristics.

Use of rays in bisecting angles

Another vital application of rays in geometry is the bisecting of angles. To bisect an angle, a ray is drawn from the angle’s vertex, creating two equal angles. This technique is used to construct various shapes that require equal angles, such as regular polygons. This intricate application of rays requires a deep understanding of geometric principles and precise calculations.

Use of rays in identifying geometric shapes

Rays are also used to identify and analyze geometric shapes. For example, rays can be used to identify parallel lines, which are lines that never intersect. In addition, rays can be used to identify perpendicular lines, which are lines that intersect at a right angle. This complex use of rays requires a deep understanding of geometric concepts and meticulous attention to detail.

Use of rays in solving geometric problems

One of the most significant applications of rays in geometry is the solving of geometric problems. Rays are essential in solving geometric problems, such as the Pythagorean Theorem, where they are used to construct right triangles and determine the length of their sides. Additionally, in circle geometry, rays are used to identify tangent lines, which are lines that touch a circle at a single point. Solving complex geometric problems requires a high degree of mathematical proficiency and a thorough understanding of geometric principles.

Applications of Rays in Trigonometry

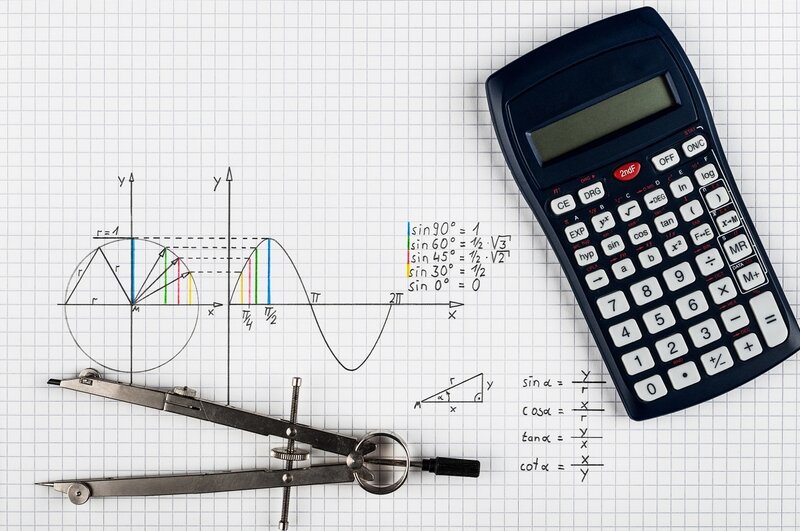
Trigonometry, an intricate branch of mathematics, delves into the intricate relationships between angles and sides in triangles. Its importance transcends multiple disciplines, including engineering, physics, and astronomy, and is utilized in a diverse array of real-world applications. 

One of the most critical concepts in trigonometry is the use of rays to define and calculate the three fundamental trigonometric functions, sine, cosine, and tangent. In this section, we will explore the complexity of the use of rays in trigonometry and how they provide the foundation for advanced problem-solving and modeling.

Use of rays in defining sine, cosine, and tangent

Defining sine, cosine, and tangent involves using rays that intersect the unit circle, a circle of radius 1 centered at the origin of a coordinate plane. These rays provide multiple perspectives on the intricate relationships between angles and sides in triangles. 

The ray that starts at the origin and intersects the circle at a given point is called the terminal side of an angle, and the angle itself is measured in standard position from the positive x-axis to the terminal side. By utilizing rays to define these functions, we can gain a deeper understanding of the intricacies of trigonometry and its multifaceted nature.

Use of rays in calculating trigonometric functions

Rays are not only crucial for defining sine, cosine, and tangent but are also fundamental in calculating these functions. Once an angle is measured, trigonometric functions can be calculated using the coordinates of the point of intersection on the unit circle. 

The sine of an angle is equal to the y-coordinate of the point, the cosine of an angle is equal to the x-coordinate of the point, and the tangent of an angle is equal to the ratio of the y-coordinate to the x-coordinate. By understanding the dynamic nature of these functions, we can utilize them to solve a broad range of problems in geometry, physics, and engineering.

Use of rays in solving trigonometric problems

The use of rays in trigonometry is not only limited to defining and calculating trigonometric functions, but also extends to solving complex problems. Trigonometric functions can be utilized to calculate the distance between two points, the height of a building, or the speed of an object in motion. 

They can also be utilized to model and analyze various physical phenomena, such as waves, oscillations, and harmonic motion. By exploring the intricate relationships between rays and trigonometric functions, we can gain a deeper understanding of the advanced applications of trigonometry and how it continues to shape our world.

Real-World Applications of Rays

The subtle intricacies of rays have inspired a multitude of applications, ranging from navigation, optics, and architecture, to even video game design. These applications have revolutionized and augmented their respective fields. Let us delve into the diverse and dynamic ways in which rays have transformed these fields.

Use of rays in navigation

Navigation, the art of maneuvering a vehicle or vessel from one point to another, has employed rays in a plethora of ways. These mysterious rays are used to convey the direction of movement and ascertain the position of the vessel or vehicle relative to a reference point. For instance, while navigating through water, a sailor may utilize a compass to ascertain the direction of a ray representing the vessel’s course. Thereafter, this enigmatic ray can be harnessed to calculate the vessel’s position relative to a well-known location, such as a lighthouse or a buoy.

Use of rays in optics

Optics, the study of light and its properties, has found a profound use for rays. These beguiling rays are employed to depict the path of light as it journeys from one point to another. Rays are instrumental in defining the reflection, refraction, and diffraction of light as it interacts with surfaces and traverses through different media. When designing a lens for a camera or a telescope, the path of rays of light passing through the lens must be carefully manipulated to achieve the desired image quality.

Use of rays in architecture and design

The enigmatic rays have found their way into the very foundation of buildings and structures. Architects and designers have harnessed the power of these obscure rays to represent the direction of natural light as it illuminates a space. This baffling information is used to optimize the placement of windows and openings in a building to maximize natural light and minimize energy use. Rays are also used to simulate the behavior of light in a space, which can be used to create more realistic visualizations of a design.

Use of rays in video game design

The magical and captivating world of video games has also found an innovative way to incorporate rays into its design. Video game design, the art of creating virtual environments and interactive experiences, has embraced the utilization of rays to simulate the behavior of light and sound in a virtual environment. The incredible ray-tracing algorithm has been employed to simulate the reflection and refraction of light in a 3D environment, which can create more realistic and immersive virtual environments that enhance the gaming experience.

Conclusion

In conclusion, rays are an important and versatile concept in mathematics that is used to describe and solve problems related to lines, angles, and shapes. From basic geometric constructions to advanced trigonometric calculations and real-world applications, rays are an essential tool for understanding and working with mathematical concepts. By exploring the various applications of ray in math and beyond, we can gain a deeper appreciation for the elegance and utility of this simple yet powerful mathematical concept.